Misc. Questions

Scalene triangles have all sides of different sizes and all the angles of different sizes. To help you remember Scalene sounds line "scale" like dragon or fish scales, fish and dragons are ugly, and so are these triangles, ugly things are nonsymmetrical, so this is as ugly as you can get for a triangle!

Ok, so we need to find the angle MBD, that is the bottom right angle, the one at B.

First step let's draw a diagram:

Next, we can calculate the missing angle on the left-hand side triangle. The sum of all the angles within a triangle must sum to 180 degrees, so 180- (78+56) = 46º

The triangle on the right-hand side will have the same angle opposite to this, this is called a vertical angle, it's like the angle seen in a pair of scissors. I don't think you will need to NAME this angle, but we can note that it is 46º

As we now know 2 angles in this triangle, we can calculate the last, as the sum of all angles within a triangle must be equal to 180º

This is a very difficult problem, luckily it's set, which means every time it comes up it is the same. If you can memorize the steps, then you can get the points. I, however, would skip this and only give it a go if I had the time. It seems to be a honey trap; an interesting question that if you just had a few more minutes you could solve. It serves only to rob you of your precious time that you should be dedicating to easier questions. A timed exam is just as much about resource allocation (time and energy) than subject knowledge.

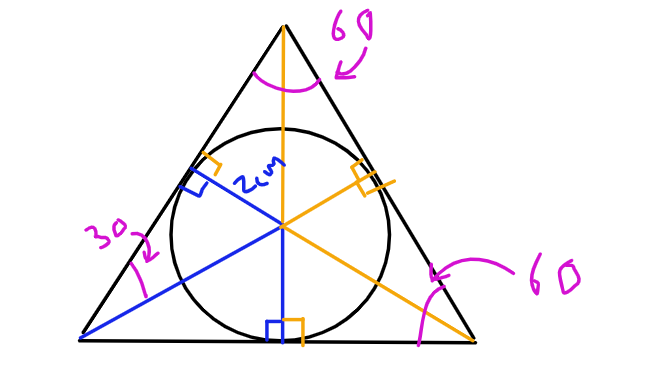
First we can split the big triangle into smaller triangles

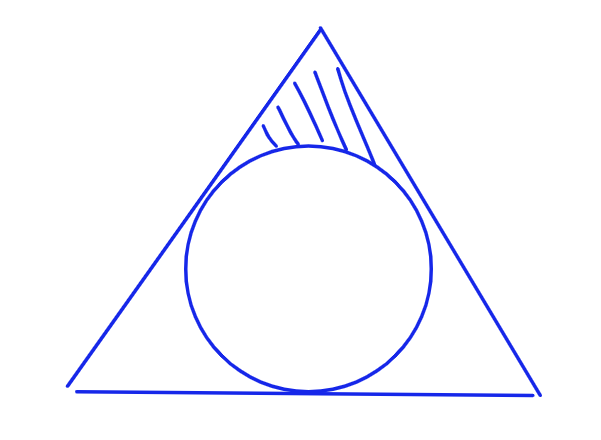
We are only looking for this top section:

Let's take one of those small triangles from the first image. They form small right-angled triangles. Once we can get right-angled triangles then we can use SOH CAH TOA and Pythagoras to calculate what we need. As we know this is an equilateral triangle, we also know the angle  at the point must be 30º

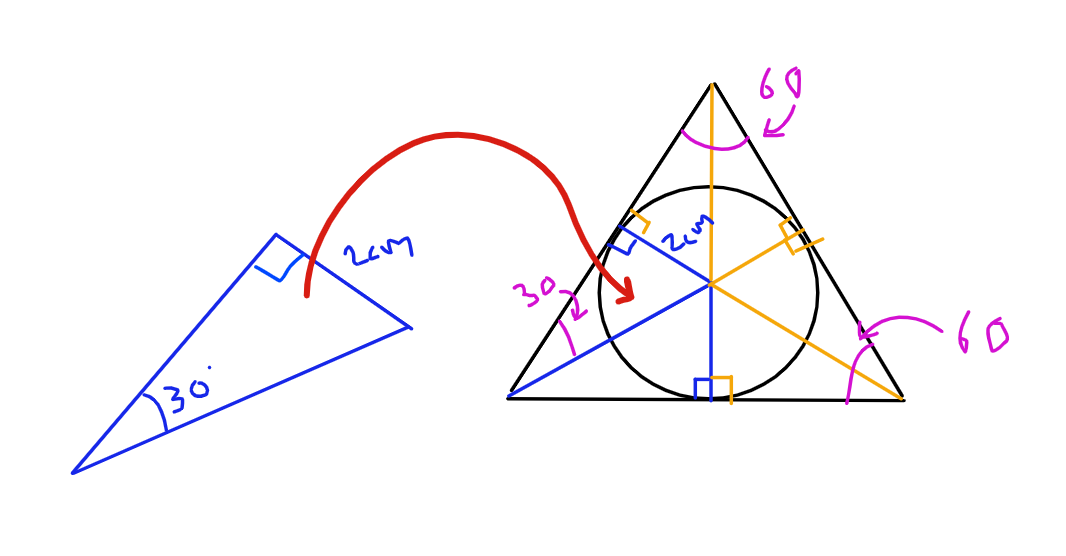
So this little triangle is the one we will be working with. We need to find its area, we need to use SOCAHTOA to get the "base"

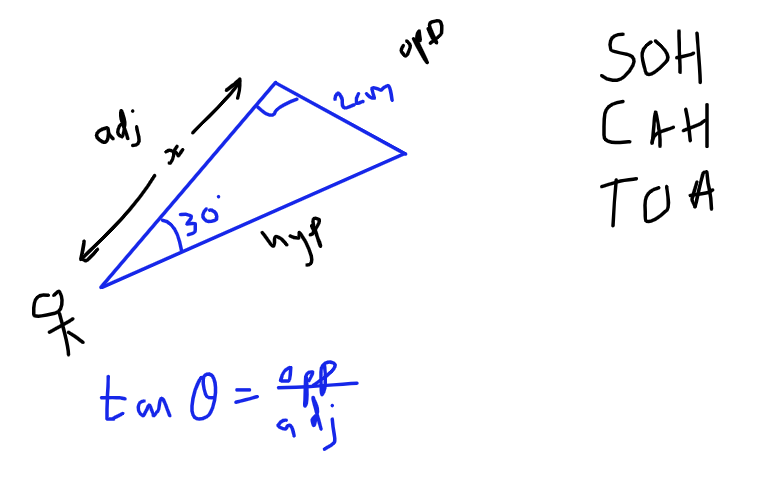
Let's substitute the values we do know, and then transpose to find x:

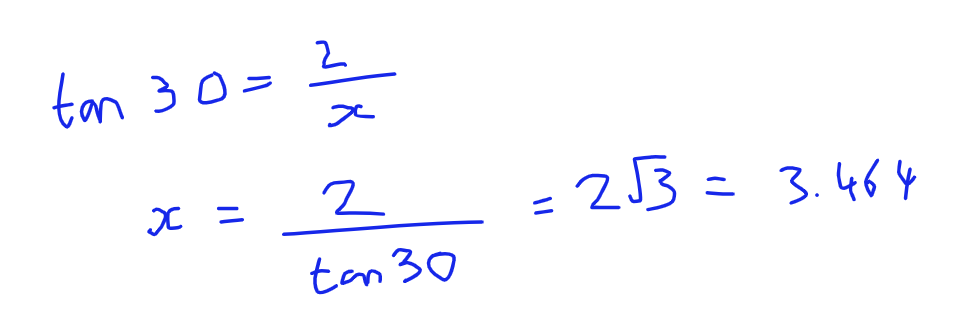
Now we know the length of the side we can calculate the area of one small triangle, then we can find the area of all 6 small triangles, which make up the big triangle (this is a bit of a roundabout method, but I wanted to try to keep it conceptually simple!)

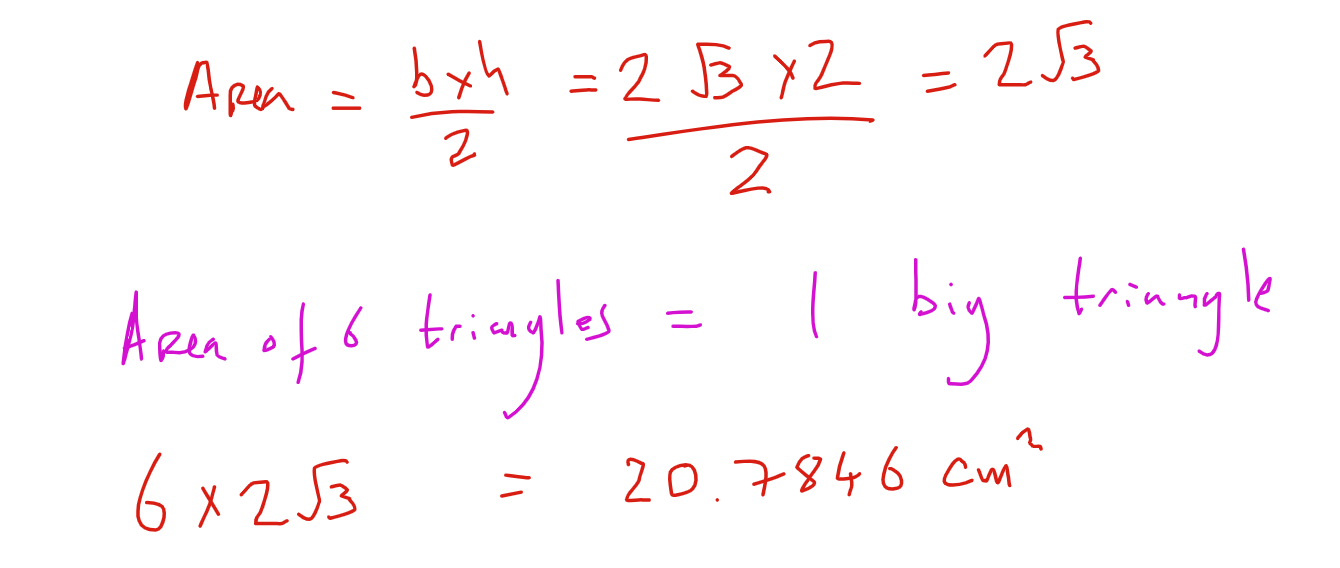
Now we have the area of the BIG triangle, we can subtract the area of the circle, effectively cutting it out: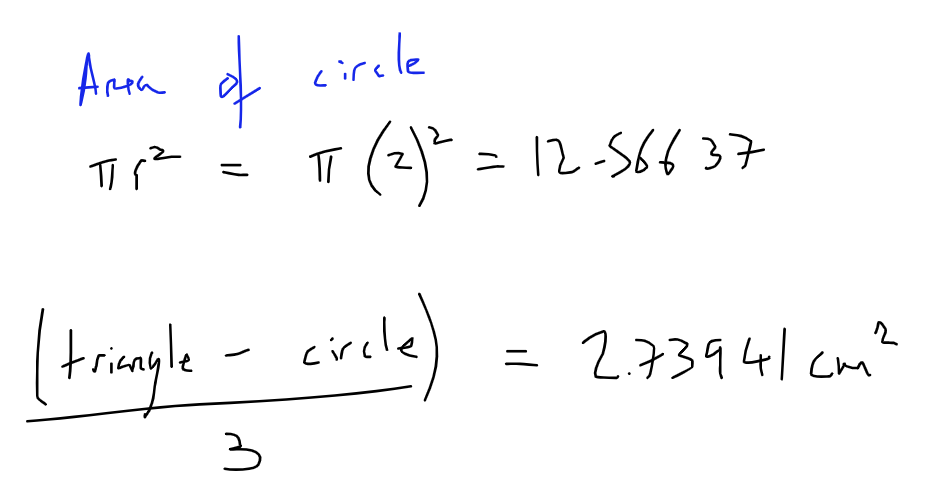

Finally, we divide by 3, as we only need a third of the big triangle.

Again this is a very hard question!