Quiz June 2022 (GES 1)

This is a substitution question, so lets rewrite the exercise with the respective values for each letter:

At every step, we should calculate what we can, so it will be simpler to handle:

Collect like terms, so we will add 3x to both sides, it's okay to equal zero!

Isolate the x term (subtract 15 from both sides), and then we can divide by 19:

First lets convert these mixed numbers into top-heavy fractions:

now let's make common denominators by cross multiplying, and then we can add the result:

now we can multiply tops and bottoms. Then as they are both factors of five, we can simplify by five, your calculator will do this for you! I just wanted to make every step explicit!

Let's transpose this to make "a" the subject, first we can subtract "ut" from both sides:

Then we can remove the 1/2 if we multiply both sides by 2

Let's divide both sides by t^2

and we are done!

It is strange that this question has "x" in it, but as the "x" is in each term we can effectively ignore it and treat this as a fraction question. So as always we need common denominators, we could do everything at once, but let's do it in small steps, starting with the first two terms. We will cross multiply, and combine the terms:

now we can work on the last two terms, again cross multiplying and combining the terms. At the end, we can leave it as a top-heavy fraction as the question doesn't specify, or we can turn this into a mixed number:

Ok, so admittedly on this one I cheated, I drew the graph on a computer. But as always it's harder than it seems to draw by hand. They have selected weird points, so we have to first work out our spacing on the y axis. Then you will get points for;

• x on the horizontal axis, and y on the vertical axis
• equal spacing on both axes
• appropriate spacing to clearly show the points
• line of best fit drawn through points
• EVERYTHING WITH A RULER!!!

Not much to this one, when they say "law" they mean the equation of a line, as we are talking about a straight line, there isn't much more to it that just y=mx+c

Let's calculate the "m" value using the m equation shown below. This can also be done using rise over run. we can see for every one step we take in the x direction we take 0.3333 of a step in the y direction.

The "c" is the y-intercept, this can clearly be seen both in the table and on the graph, where c =-1

Then we just put it all together:

I think the hardest part of this question is understanding what they are trying to say. To cover our backs let's state a general Pythagoras theorem, and then make it relevant to the question by substituting all the values that we can:

Ok, so time to solve the setup from part a

Let's set this up as a SOH CAH TOA. I will draw a little guy at the angle I am trying to find, then label the sides with respect to him (and the angle):

Now, as we have Opp and Hyp, we select the SOH:

Plug in the values and solve:

Scalene triangles have all sides of different sizes and all the angles of different sizes. To help you remember Scalene sounds line "scale" like dragon or fish scales, fish and dragons are ugly, and so are these triangles, ugly things are nonsymmetrical, so this is as ugly as you can get for a triangle!

Ok, so we need to find the angle MBD, that is the bottom right angle, the one at B.

First step let's draw a diagram:

Next, we can calculate the missing angle on the left-hand side triangle. The sum of all the angles within a triangle must sum to 180 degrees, so 180- (78+56) = 46º

The triangle on the right-hand side will have the same angle opposite to this, this is called a vertical angle, it's like the angle seen in a pair of scissors. I don't think you will need to NAME this angle, but we can note that it is 46º

As we now know 2 angles in this triangle, we can calculate the last, as the sum of all angles within a triangle must be equal to 180º

This is a very difficult problem, luckily it's set, which means every time it comes up it is the same. If you can memorize the steps, then you can get the points. I, however, would skip this and only give it a go if I had the time. It seems to be a honey trap; an interesting question that if you just had a few more minutes you could solve. It serves only to rob you of your precious time that you should be dedicating to easier questions. A timed exam is just as much about resource allocation (time and energy) than subject knowledge.

First we can split the big triangle into smaller triangles

We are only looking for this top section:

Let's take one of those small triangles from the first image. They form small right-angled triangles. Once we can get right-angled triangles then we can use SOH CAH TOA and Pythagoras to calculate what we need. As we know this is an equilateral triangle, we also know the angle  at the point must be 30º

So this little triangle is the one we will be working with. We need to find its area, we need to use SOCAHTOA to get the "base"

Let's substitute the values we do know, and then transpose to find x:

Now we know the length of the side we can calculate the area of one small triangle, then we can find the area of all 6 small triangles, which make up the big triangle (this is a bit of a roundabout method, but I wanted to try to keep it conceptually simple!)

Now we have the area of the BIG triangle, we can subtract the area of the circle, effectively cutting it out:

Finally, we divide by 3, as we only need a third of the big triangle.

Again this is a very hard question!

In order to calculate the acceleration, we are going to use a SUVAT. This is angular acceleration, and there is an angular set of SUVAT equations, but as they are essentially the same as the linear ones, and to save us having to learn more formulas than needed, let's just use regular SUVAT.

First, we will need to convert the units in the question into the Units required in the answer. We need the acceleration to be in Rads/sec ^2, so let's convert the initial velocity and the final velocities from RPM to Rads per second:

We turn Revs to rads by multiplying by 2pi, and then 1 minute into one second by dividing by 60. (again there are shortcuts for this, but as we spend ALOT of time converting units, I find this method is easier to remember, understand, and check).

Now we can solve that SUVAT:

We can think of linear velocity in the same way as speed.

So we need to know the distance traveled and the time taken to cover that distance. The distance travelled by a point on the perimeter would be the circumference of the circle.

Let's explain the diagram above. we are given the velocity as 1000 revolutions per minute. The distance travelled in one revolution is the same as the circumference of the circle, this is given by Pi*D (pi*0.3) and we know that there are 60 seconds in a minute, so let's write it like that. Velocity is usually given in meters per (one) second, not sixty, so let's fix that by dividing it down:

As there is no friction, and it is a horizontal surface, this becomes a VERY easy question, we can use F=ma to solve for the acceleration:

A simple SUVAT is needed to solve this:

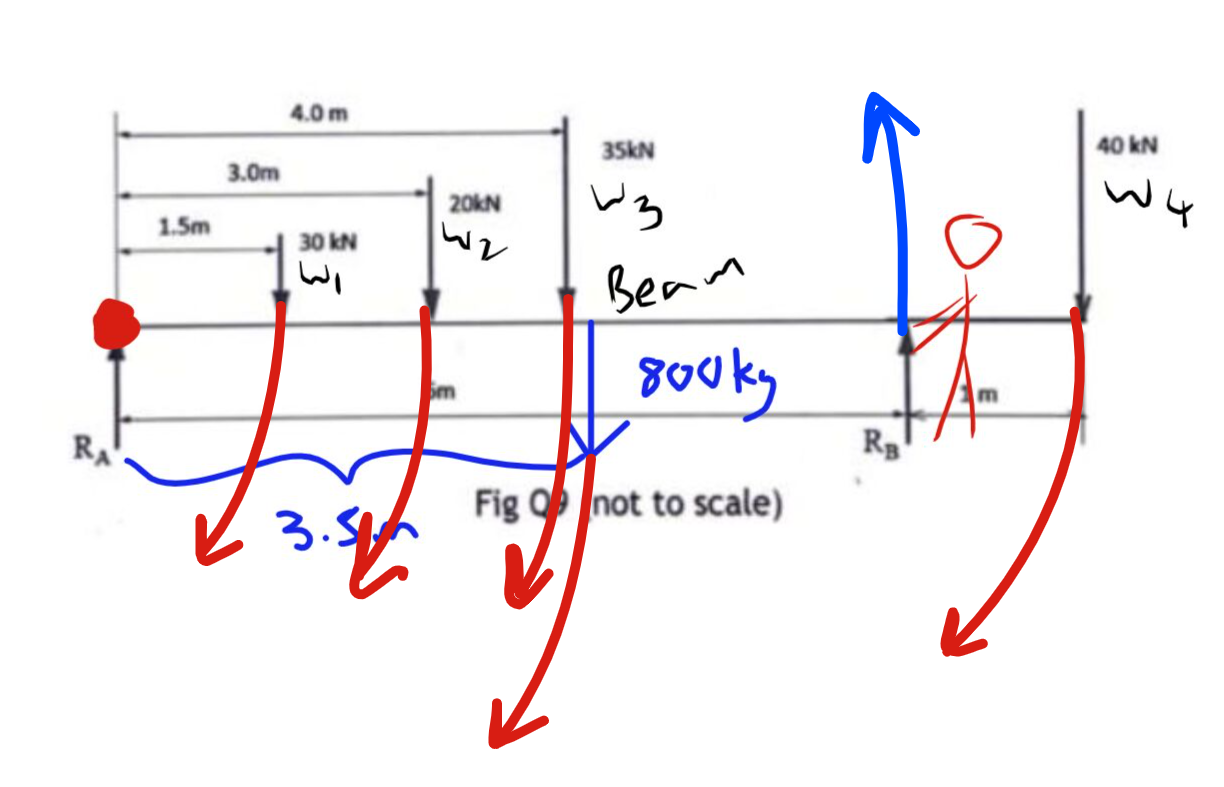
This is a beam question, first we will draw a picture of it so we can see what is going on. We also need to label each of the weights, masses and forces acting on the beam, We will give them nice easy names, such as W1, W2, W3, UDL for uniformly distributed loads, BEAM (for the beam mass) and RB for the Reaction force at B.

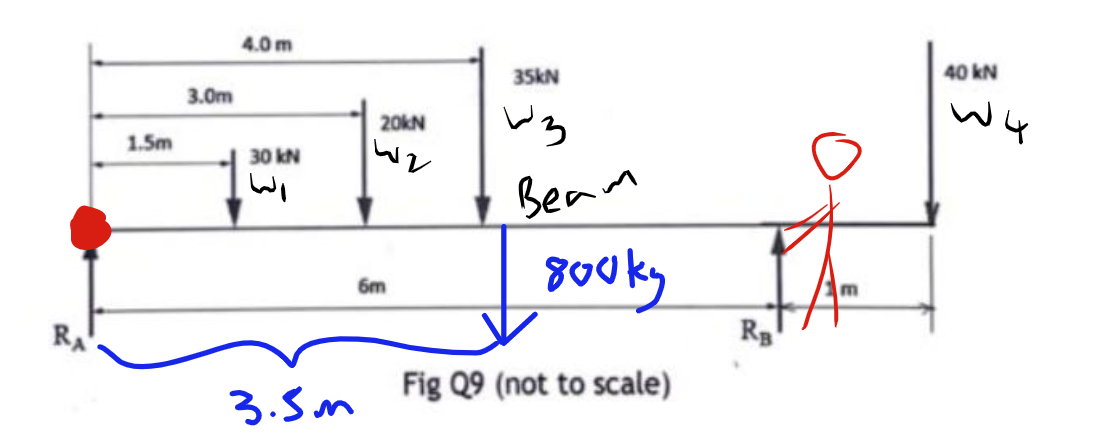
I have also drawn a little guy standing at B, this is help me conceptualize what is going on. I imagine this as being a table, now imagine lifting the table up at where the support B is at, the force you would feel by lifting the table by just a little bit would be the force at that point. We could also walk around and lift the beam from point A, this would be the force experienced at point A.

Luckily for us, we only need to make this calculation once, and then we can get both RA and RB due to a few concepts in physics, we will state these now for the sake of the examiner, we have to state all equations and theorems used:

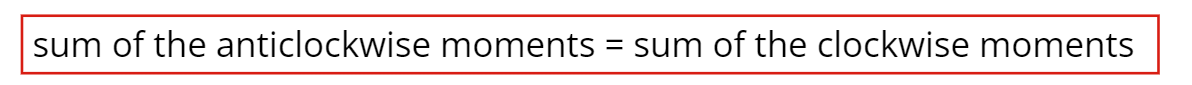
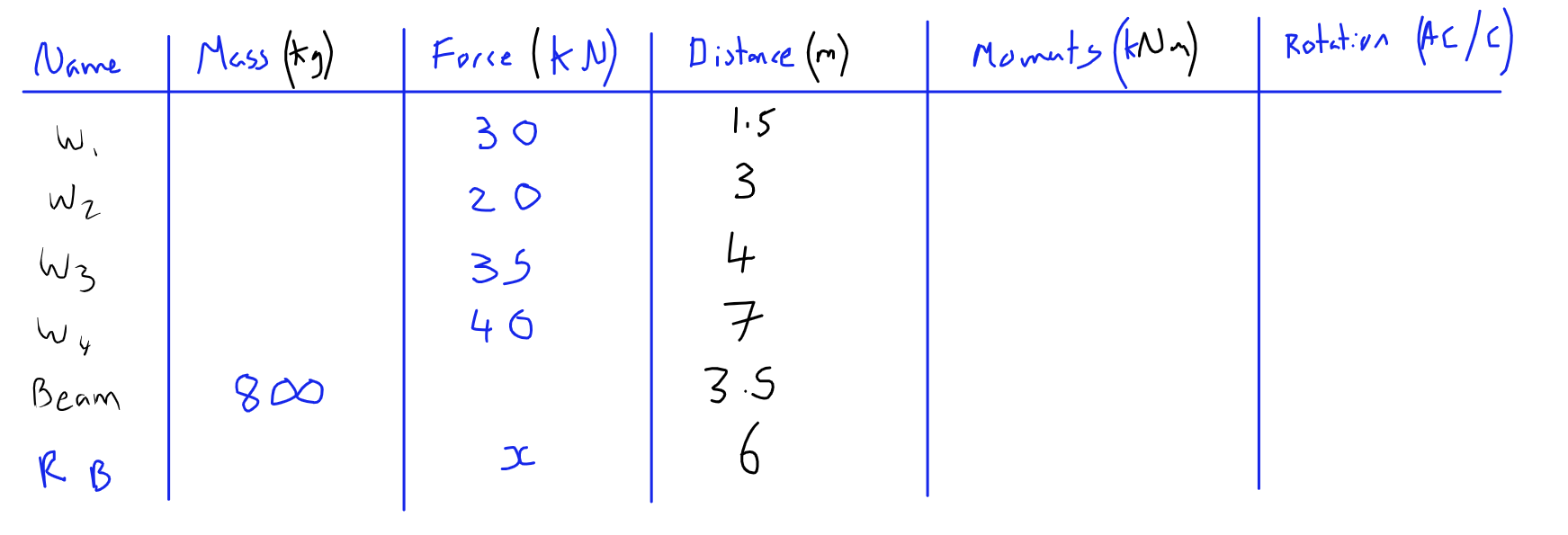
Now lets get to building a table with all of this information, I find it best if you can make a mnemonic with the table headings:

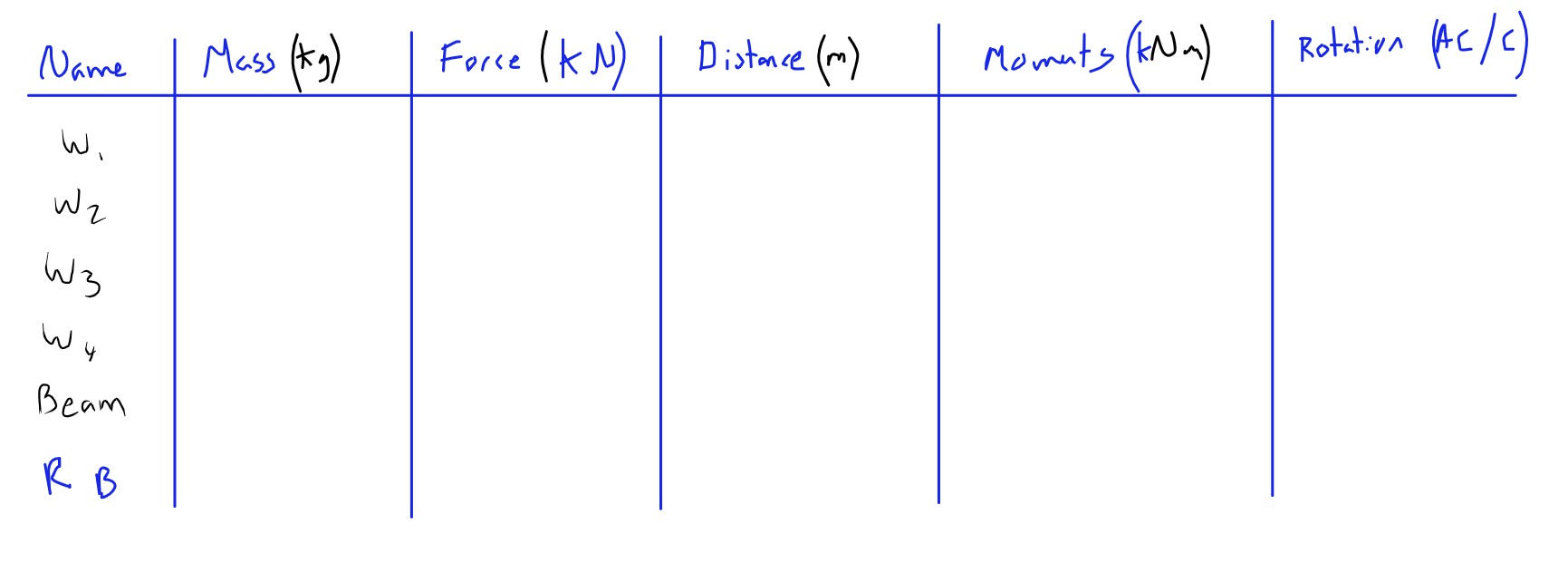
Lets fill in what we already know, this is "taking moments about A" which means we treat A as the pivot, this table is so good it doesn't matter how we alter the question, it will always work.

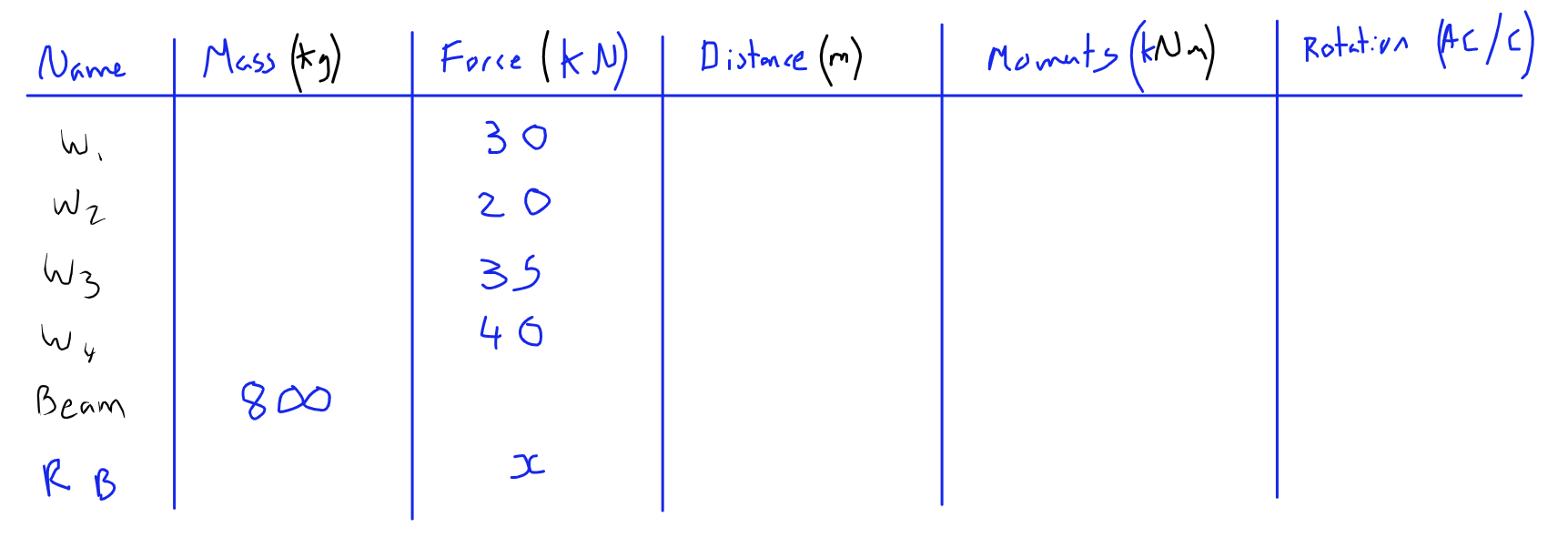
Will fill in the Mass in KG for those that we have, then to fill in the force column, we multiply by gravity (9.81).

I have used "x" as the reaction force at B as this is the variable we are solving for, we can carry it through the rest of the process without any problem.

Next, we need to fill in the distances from the pivot, it doesn't matter if it's to the LEFT or RIGHT, the direction of the turning force will be taken into account in the last column (Rotation). Getting the distances correct actually seems to be the most difficult part of this!

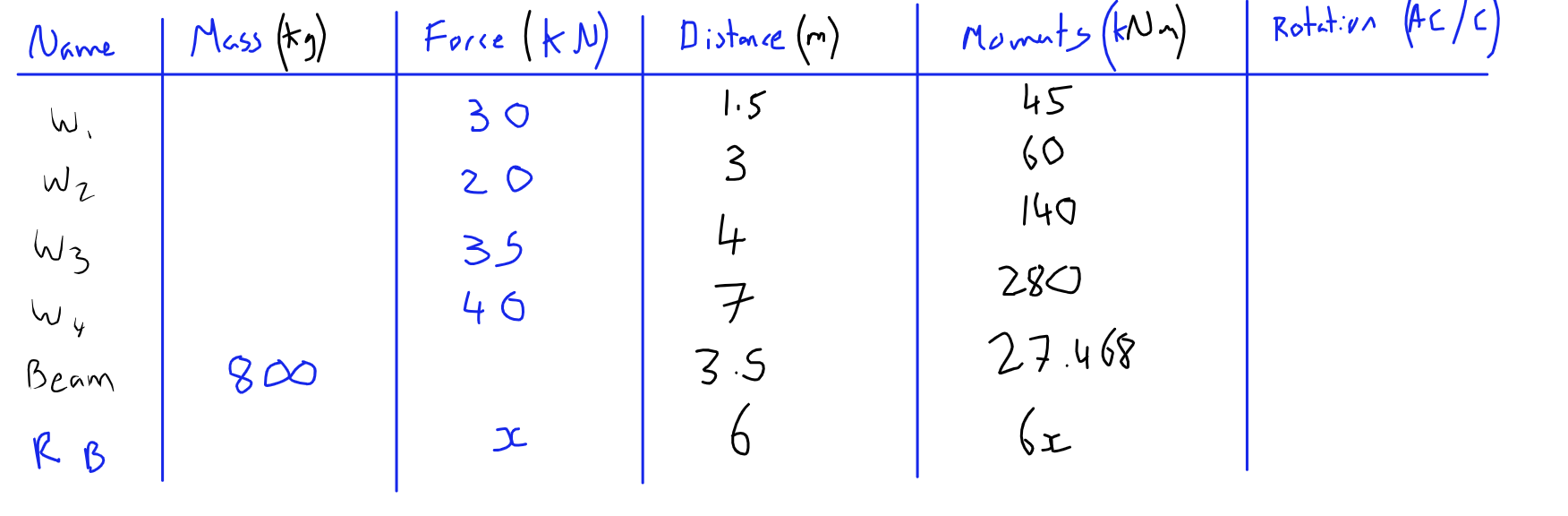
Next moments are calculated by multiplying the force by the distance:

Finally, we need to consider the diagram, and see if the beam was left to rotate freely, which way would each of the forces wish to move. I have coloured clockwise movements in RED and anticlockwise movements in BLUE. as you can see this poor guy is working against ALL of the other forces!

Now we can finish off our table, and then get to using it: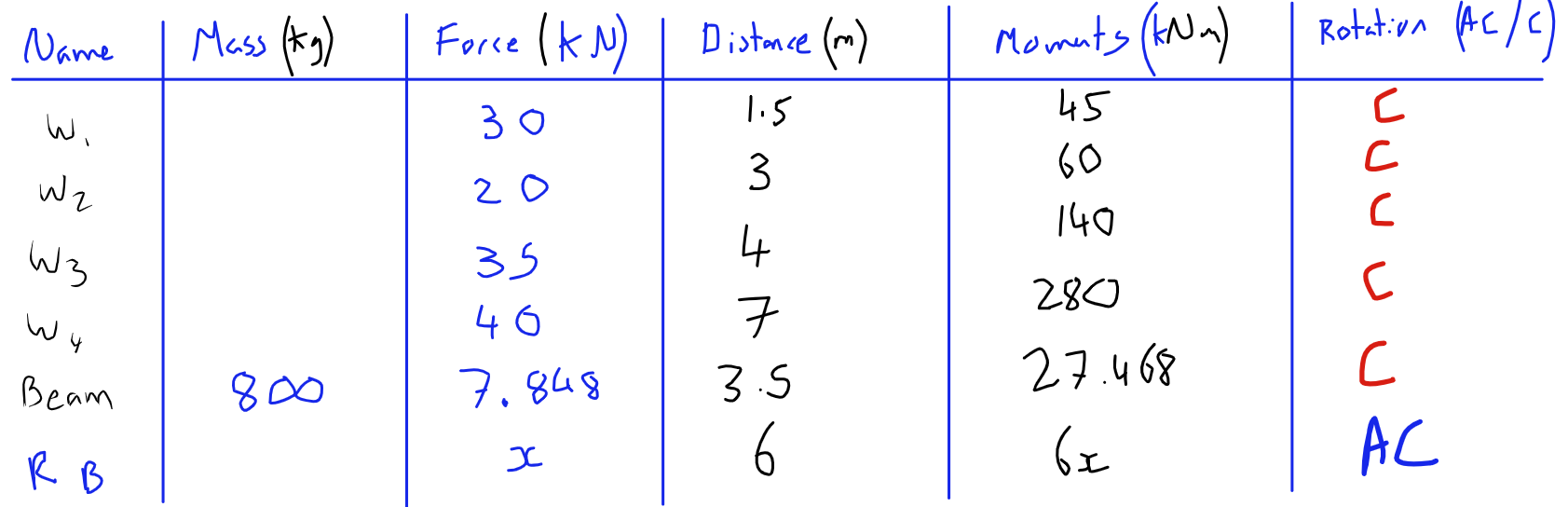

As previously stated, the Sum of the anticlockwise moments must be equal to the sum of the clockwise moments. This is because beam is not flying around all over the place (or spinning) If the forces were not in equilibrium it would be moving. So, using the last two columns, and this statement, we can say the following, and solve for x:

So now we have the Reaction force at B. Now using the other previously mentioned statement (the sum of the downwards forces must equal the sum of the upwards forces) we can solve for the reaction for at A. This is because the beam is not moving, so the push down must be equal to the push upwards:

We just have to be careful to pick out the correct numbers, we need the downwards forces, which is found in the 3rd colum.

The force ratio is the force lifted (or the force we are wanting to apply, usually it is lifting, sometimes pushing) divided by the force we apply (the input force). I remember this as it is ALWAYS (for these tests) the larger number divided by the smaller number. The result, say 10, is the magnification effect the equipment has on your force, so I can lift a force ten times greater than the force I apply.

The velocity ratio (aka movement ratio) is the distance I have to move in order to move the load, divided by the load. Think of this as peddling a bike uphill in low gear, you have to peddle a whole bunch in order to move very slowly uphill! Again it's always the larger number divided by the smaller number, it's just in this case it is actually the other way around to the force ratio, again to avoid confusion, big over small.

The efficiency of the machine is given by the Force ratio divided by the Velocity Ratio. In order to remember this, I use the acronym EFM (Efficeny =Force ratio / Movement ratio). These questions are always together,  so it's the first thing I write down.

One more thing to help me remember is that you cannot have efficiency greater than 100% (as a percentage) or greater than 1 (as a decimal), so the smaller number always needs to go on top. If you end up with a 150% efficient machine, you have got it the wrong way round!

Efficiency can be given as a percentage or a decimal, they are both valid.

You cannot have a machine that is 100% efficient, this is a law of physics, You always lose energy to a system through unwanted losses, such as heat, friction, and sound. You cannot have 100% and you certainly cannot have more than 100%! These are perpetual motion machines!

This is one of my favorite questions, it combines stress with some interesting geometry. First, we will draw a picture:

The stress equation is easy enough, its the force divided by the area:

The interesting part of the question is the area over which the force is exerted. The area is the cross-hatched side of the cylinder in the diagram above. This is the area that used to stick the round that we just punched out, into the plate. We need to calculate the curved surface area of the cylinder.

Now we know our area, we can calculate our stress. This can be given in N/m^2 or N/mm^2 whichever is more appropriate:

First, lets draw a diagram:

Next, we need to look at the vertical and horizontal forces. The force being applied is at an angle, so let's break that down, I will label the vertical y, and the horizontal x

As the angle is upwards, this is actually pulling our box up, and making the friction force less, we can use SOH CAH TOA to solve for both the horizontal and the vertical:

Ok so we have split up the diagonal force into the vertical (pulling up) and the horizontal (pushing along, or driving force). Now lets in clude gravity, which is pulling the box down.

As the pull up, and the push down are in opposite directions, we can subtract the lifting force, from the force due to gravity to find the net vertical force:

Lastly, we can calculate the coefficient of friction, as the box is "just" in motion, we know the friction force must equal to the pushing force: